Motivation
Recently, as my freelance contract expired and I have an upcoming vacation, I decided to use my free days to have some fun writing code and experimenting a bit. I got neck-deep into Function Programming again (I will have a series of posts on my OCaml journey and maybe even about the Programming Languages course I am doing) as I enjoy it more and find it easier to reason with.
Naturally, as a JS/TS developer of many years, I decided to try to implement pattern matching myself in TS. Taking some language functionality and trying to implement it from scratch is a fun and challenging way to test your knowledge of the language constructs and structure. However, before this experiment, I only tried reimplementing things that already existed in JS/TS such as redux and redux-thunk, some parts of React and so on. That said, I found out that implementing something that doesn't exist is way more thrilling and fun.
Some notes
Before we start, I am very happy that there is a pattern-matching proposal and that soon it may be implemented into the language. I believe TS also is getting support soon which is pretty exciting. However, with this attempt, my goal was to try myself and see if I understand the concept of pattern matching as well as the language I used for work for quite a while now. As I am "under the influence" of OCaml, I tried to design my implementation as close as I can to the OCaml. With this said, let's dive into it, shall we?
Problem statement
As I already mentioned above, I wanted an implementation that is going to be as close to OCaml syntax as I can get. Firstly, we will try to implement the minimal PoC and then try to build on top of it. So, first of all, let's see a couple of simple examples of pattern matching in OCaml to get the hang of the syntax. First and foremost, we should be able to match a constant value. Let's take a look at the code below:
let rec power x n =
match n with
0 -> 1
| 1 -> x
| _ -> x * power x (n - 1)
The 3rd and 4th lines look to match the constant values of 0 and 1. That is to say, if n is 0 then return 1 else if n is 1 return x.
Another very important "feature" we will want for our pattern-matcher is the ability to match anything or as OCaml calls it a "wildcard". The wildcard, as you can see from the example above, is denoted with the _ symbol.
One more simple pattern is a variable name. It acts a lot like the wildcard pattern except it also initializes the variable of a given name.
let square_funny x =
match x with
y -> y * y
This pattern with match the value of x and initialize y with that value, which then will be used to return the square of x (which is also y :D)
Next, and maybe one of the most powerful and most common uses of pattern matching would be matching a list with the help of the :: (pronounced cons) operator.
let rec length xs =
match xs with
(* If list has no elements return 0 *)
[] -> 0
(* Else it has head aka the first element
and tail aka the rest of the list
*)
| h::t -> 1 + length t
As you can see in the second case the matched pattern creates 2 variables h and t. h will hold the first element of the given list and the t will hold the rest of the list. For example, when xs is [1; 2; 3], the match will initialize h with 1 and t with [2; 3] (Question: What would h and t be for the list ["hi"]?)
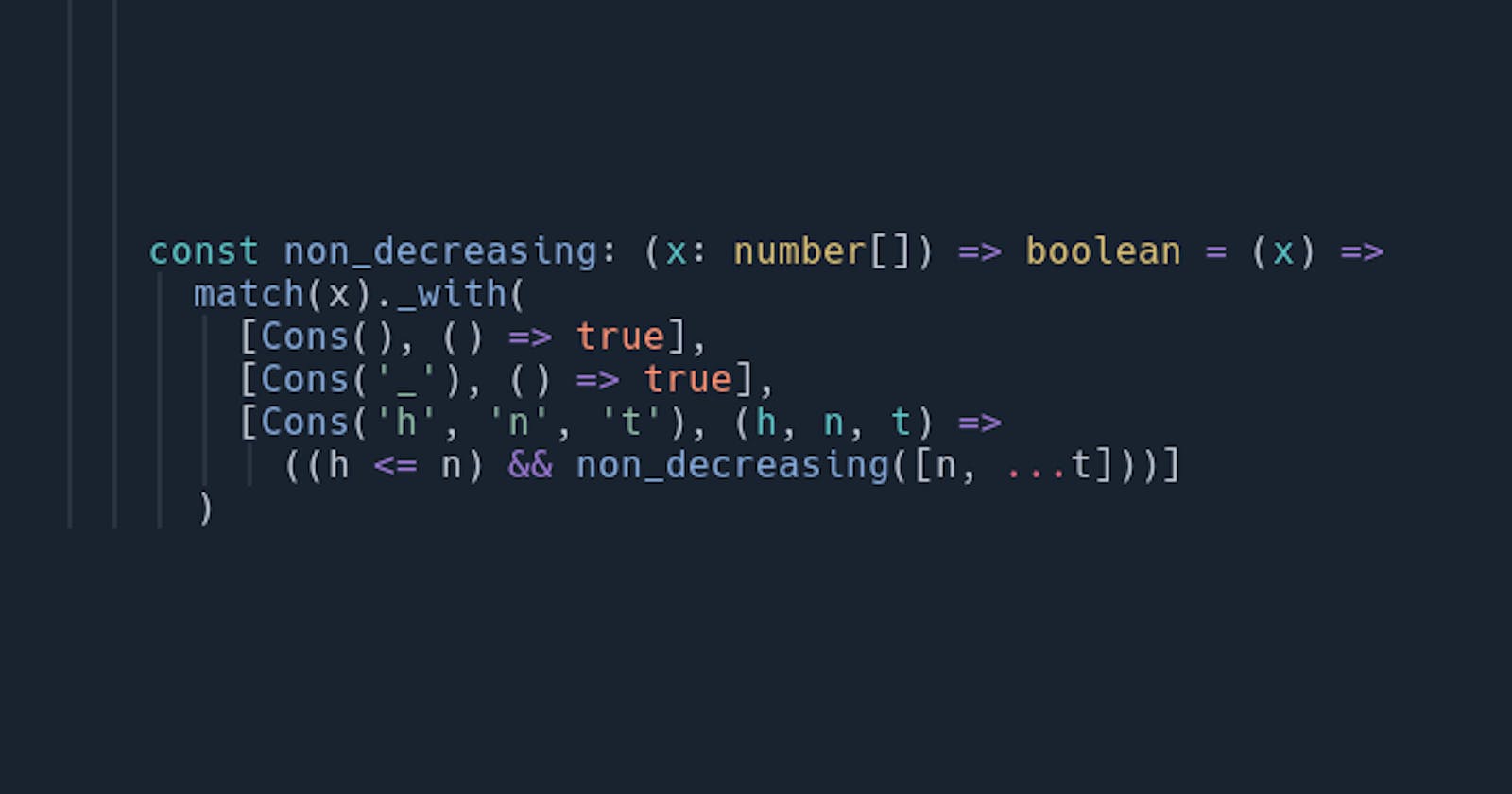
The neat part of this is that cons can be used as many times as someone wishes, as long as the pattern is matching. To illustrate this idea better let's look at a function that checks if the list is continuously non-decreasing.
let rec non_decreasing xs =
match xs with
(* If list has 0 elements, it's non-decreasing *)
[] -> true
(* If the list has 1 element it's still non-decreasing *)
| [_] -> true
(* Else it has head aka the first element
neck aka the second element
and tail aka lthe rest of the list
*)
| h::n::t -> h <= n && non_decreasing (n::t)
(*
NOTE: We could merge first two cases into one with a pipe like this:
[] | [_] -> true
but for the sake of simplicity we will consider the above version
*)
So, as you can notice in this case we don't extract just one but TWO elements at once and initialize t with the remaining list.
These would suffice for us as a PoC, so let's summarize what we need.
Initial design thoughts
I wanted a syntax close to OCaml. I cannot have the match and with as keywords so what we are going to do instead is to have a match function that can be chained with .with like this
match(value).with(
// patterns
)
However, it turns out that with is a JS keyword, so we will use _with.
Now what about the patterns that we need to feed to _with? It can be an arbitrary number of pairs of type [<pattern>, <expression>] where <expression> is something that should be executed in case the pattern is matched. So, in JS/TS sense, the expression will be a function. Now what would our patterns be? I would very much like them to be premade constructors/functions which can be used to match things under our control. So, the wildcard would be a value named _, constants would be something like Const(5) and Variable(x) and Cons(h, t) would be used for variables and lists respectively. In the wildcard case, we already have a value, in the other cases we need functions Const, Variable and Cons which take some arguments and return data similar in type to the value of _.
So, without further ado let's get started!
Initial code
Values we match
Let's start with trying to write some initial version of the match function. It will take one argument. In our PoC, let's take value to be either string, number or boolean or array of either of these three:
type Matchable = string | number | boolean | Matchable[]
Notice the recursive type definition. This is a common practice in the Functional Programming world and it makes sense here too. It's all fair in our case to have an array of either of those 3 primitive types or even an array of an array (...of an array) of those primitives.
The match function
Having matchable as our type for the value argument, let's write our match function so far to see what we need.
const match = (value: Matchable) => {
const _with = () => {} // TODO: Write with
return {
_with
}
}
On to the next thing! What signature should we give to _with? Well, it can have as many arguments as the user wants, but they all should be pairs of [<pattern>, <expression>]. So the type of _with's argument should be:
type PatternAndCb = [Pattern, (...args: any) => any]
// Type of _with's argument is PatternAndCb[]
The _with function should go over all the PatternAndCb pairs one by one and should check if the pattern matches the value. If so, it should take the list of bindings that it creates and apply it to the callback function. After applying it to the callback, _with should return the resulting value to the user. If no pattern matches, it should throw an error of some kind, letting the user know that nothing matched. Let's write this logic quickly using Array.prototype.findIndex:
const match = (value: Matchable) => {
const _with = (...patterns: PatternAndCb[]) => {
// Instead of reduce/forEach or a for loop we use findIndex
// for short circuiting. I find this solution to be more elegant
let bindings = null;
const found = patterns.findIndex((checkedPattern: PatternAndCb) => {
const pattern = checkedPattern[0];
bindings = matches(value, pattern);
if (bindings !== null) {
// We found a match so we can stop
return true;
}
// The pattern didn't match, go to the next one
return false;
});
// No pattern matched, so let's throw an error. As usually pattern
// matches are made exhaustive using the wildcard, let's give that
// as a hint to the user in the error message.
if (found === -1) {
throw new Error("Pattern match failed. Maybe you forgot _?")
}
// Use the pattern with found index. The second item
// is the callback
const callback = patterns[found][1]
return callback.apply(null, bindings || []);
}
return {
_with
}
}
The code here is pretty simple: we call the function matches which checks if a single pattern matches the value or not. If the pattern does match, the matches function returns a list of bindings the match created, otherwise, it returns null. We then null check to see if there are any bindings. In case of bindings not being null, we know we found a match. In that case, we terminate the search for a matching pattern as we return true, because findIndex will stop when one of the list elements passes the check. If matches returns null we move to the next pattern in the list until we either find a match or see that no pattern matches the value. If no match is found, we throw an error otherwise apply the bindings to the matched pattern's callback.
Defining the patterns
Now, before moving to the writing of the function matches let's define our patterns. As we already decided, we need 4 different types of patterns Cons, Variable, Const and the wildcard _. The first three are functions that take some arguments and return something of the type Pattern. The 4th one is a value of type Pattern. The Pattern type should keep the data passed to it and also a way to read its type. So I made the type Pattern to look like this:
type Pattern<T = any> = { _patternType: string, _data?: T };
It will hold any data of the given type T and the _patternType field will be used to do the matching. So let's now use this to define our patterns.
// Const is a user specified value. It can be of any type T
// so we pass that type to the Pattern
const Const: <T>(a: T) => Pattern<T> = (a) => {
return {
_patternType: 'ConstP',
_data: a
}
}
// Variable doesn't need to store any data
// It just has the name of the binding
// NOTE: Read on to the caveats section to discuss
// one issue with this.
const Variable: (a: string) => Pattern = () => {
return {
_patternType: 'VariableP',
}
}
// Cons, as discussed above can take arbitrary number
// of elements out of the array, so we don't really know
// how many arguments there are. Fortunately, the spread operator
// comes to the rescue.
const Cons: (...args: string[]) => Pattern<string[]> = (...args) => {
return {
_patternType: 'ConsP',
_data: args
}
}
// Lastly, define the wildcard pattern
const _: Pattern = {
_patternType: '_'
}
Now, to do a pattern match, the user will write things like:
// let foo = ...
match(foo)._with(
[Cons(), () => console.log([])],
[Cons('h', 't'), (h, t) => console.log(h, t)]
)
// let bar = ...
match(bar)._with(
[Const(5), () => console.log('bar is 5')],
[Const(10), () => console.log('bar is 10')],
[_, () => console.log('bar is anything but 5 or 10')]
)
const square_funny = (x) =>
match(x)._with(
[Variable('y'), (y) => y * y]
)
With all this set up, we move to the most complicated yet most interesting part - the matches function.
The matching logic
Now as we have patterns and know the shape of data the patterns hold and the kind of data the values can hold, we need to write a function that takes one value and one pattern and returns a list of bindings created by the match. If the pattern and value don't match, the function should return null.
const matches: (value: Matchable, pattern: Pattern)
=> Matchable[] | null
= (value, pattern) => {
// Some awesome logic
}
Now let's look case by case at how our function should behave.
In the case of a
_pattern, any value should match, the bindings list is just an empty listIn the case of a
Variable('x')pattern, again, any value should match, creating a binding list with a single element - holding the valueIn case of a
Const(v)pattern, the value matches if and only ifvis equal to thevalue. However, no bindings are created.In case of a
Cons('h', ..., 't')pattern, the value matches if:Value is an array
Value has 1 or more elements
Value has at least as many elements as
Cons' arguments minus one. This is because all those arguments should be matched by one element of the list and the last one should be the remaining list (which can as well be empty).
In case of a
Cons()andCons('t')patterns, the value matches if and only if it has 0 and 1 elements respectively
So we just need to take those points and implement them one by one. The easier ones are at the top so let's go top to bottom:
const matches: (value: Matchable, pattern: Pattern) => Matchable[] | null = (value, pattern) => {
const {_patternType: patternType, _data: patternData } = pattern;
// If the pattern is wildcard we have a definite match, no bindings
if (patternType === '_') {
return [];
}
// If the pattern is Variable, we have a definite match, one binding
if (patternType === 'VariableP') {
return [value];
}
// Otherwise check the type of the value
switch (typeof value) {
case 'number':
case 'string':
case 'boolean':
// Match the primitives only if we have constant pattern
// holding the same exact value, no bindings
if (patternType === 'ConstP' && patternData === data) {
return []
}
// Otherwise pattern doesn't match
return null;
case 'object':
// If typeof value is object it can be an array,
// If it is, in fact, array, check if the pattern
// is the right one and do the length checks.
if (Array.isArray(data)) {
// pattern.length includes arbitrary number of elements cut
// from the beginning plus one more argument that's
// gonna be the tail aka the rest of the elements.
// So check if there are enough elements in the
// value to match the pattern
if (patternType === 'ConsP') {
const patternData = (pattern as Pattern<string[]>)._data;
const length = patternData ? patternData.length : -1;
// If we have an empty array, match the Cons()
// Also, one element array shouldn't just match the
// Cons('t') and return the tail. It should only
// match arrays with one element
if (data.length <= 1 && length <= 1
&& data.length === length) {
return data
}
// Check if array has enough elements, if it does
// take that many elements from the start and put the rest
// in the tail
if (data.length > 1 && length > 1 && data.length >= length - 1) {
return [...data.slice(0, length - 1), data.slice(length - 1)]
}
}
}
// Pattern didn't match.
return null
default:
return null;
}
}
Notice that we need to check the type of value. That's easy in the case of so-called "atomic" values such as string, boolean or a number - just use typeof. However, checking if the value is an array is a bit more intricate as typeof returns object when applied to an array (well, that's how the language is built). So we need to use Array.isArray to know if the value is an array.
I intentionally checked for type object and then only after if it's an array. That's because I plan to extend this PoC later to be able to work with values of type Record aka proper objects. I also plan to add support for Tuples aka matching multiple in the same match expression.
Caveats
As we saw when implementing the variable pattern, we use strings as arguments for the variable pattern. This will work well, but it assumes the correct usage of the user, which is usually not the greatest idea. The problem is, the code itself doesn't use the argument name strings, it just checks to see if the argument is there in the first place. Then, when we apply the matched bindings, we don't really use the names either, just the order.
To explain the idea better let's look at the example below:
const foo = "Hello world",
match(foo)._with(
[Variable('x'), (notX) => console.log(notX)],
[_, () => console.log("Matched the wildcard")],
)
Given our implementation, this code will work just fine, the pattern of Variable is getting matched and there is one value that needs a binding. We pass that value as an argument to the function next to it which then shows it in the console. Although the name of the argument is not an x, everything still works. This is a small issue that can be fixed but at the same time, for my idea of understanding the concept of pattern matching and translating the code to TS, it's a bit secondary.
Conclusion
That's it! Now we have a working PoC for pattern matching. The full code can be found here. I went ahead and added support for Tuples as well. I plan to write another post about it later as I add the support for objects as well.
This was very fun to implement because I solidified my grasp of TS and pattern matching with just under 200 lines of code. If you have any comments regarding the code or the post itself, you can reach me on any of my socials.
See you around! Happy coding!